Теорема пифагора совместимость: Compatibility by the Pythagorean Square (psychomatrix)

Содержание

Совместимость по дате рождения. Бесплатный расчет.

Как рассчитать в паре совместимость по дате рождения?

Во-первых, не гонитесь за 100% результатом по всем параметрам — его не существует.

Совместимость по дате рождения, согласно результатам расчета, редко бывает абсолютно положительной или абсолютно отрицательной.

Ведь отношения — это не такая тривиальная вещь, чтобы их можно было охарактеризовать одной общей цифрой, итоговым процентом или, скажем, «совместимы / несовместимы». Отношения — тема очень сложная и многогранная, поэтому и предложенный расчет не прост. Учитывайте и принимайте во внимание все полученные результаты.

Однако, автор расчета дает свои критерии совместимости партнеров:

— биоритмы / чакры: совпадают эмоциональные биоритмы (вторые чакры) и хотя бы одна пара из трех высших
— гороскоп: знаки не одинаковы, знаки принадлежат одной стихии или, если стихии разные, то это пары Земля-Вода, Воздух-Огонь
— квадрат Пифагора: характеры, семейность и темпераменты в паре не различаются больше, чем на 2 балла

При всем этом расчет не запрещает вам строить отношения, не подходящие под критерии выше. Анализируйте отношения сами, делайте ставку на стороны, которые вас объединяют с избранником, но учитывайте проблемные сферы и старайтесь их сглаживать. Все в ваших руках.

Раз уж вы оказались на этом сайте, то, наверное, так же, как и большинство его пользователей и те, кто работал над In-contri, верите в то, что дата рождения человека является чем-то большим, нежели просто набором цифр дня, месяца и года его появления на свет. И, наверняка, уже сталкивались с огромным количеством информации, которую можно получить о себе, зная только эту дату. Расчет совместимости In-contri — одна из удачных попыток собрать в одном месте самую точную, объективную и четко изложенную информацию в частности о совместимости по дате рождения. Считайте, анализируйте, экспериментируйте и делитесь с результатами. Администратор и подписчики группы Вконтакте всегда с интересом обсудят ваш опыт.

Какие совместимости не считает In-contri?

— по именам
— по цвету глаз
— по цвету волос
— по форме носов и ушей
— …и прочих частей тела
— синастрию

Пожалуй, со всеми пунктами, кроме последнего, ситуация очевидная — они не являются «координатами» человека, каковыми являются его день, месяц и год рождения в системе счисления времени. Кстати, система эта, как уже поднималось не раз в ответах на отзывы, будучи по сути неизменной, но преподносимая в разной терминологии, действует со времен зарождения человечества и известна, начиная с шумеров.

Ситуация с синастрией немного сложнее. Во-первых, синастрия служит как бы добавочной информацией к базовой соместимости знаков партнеров. И ошибочно, как преподносят во многих источниках, считать синастрию главным критерием. Во-вторых, в этом расчете очень высок шанс на получение абсолютно недостоверных результатов из-за того, что, как минимум, мы сами-то не всегда точно знаем свой час рождения (только со слов родителей), а что говорить за партнера. Поэтому мы не отвергаем синастрию, но считаем, что более-менее адекватный результат по ней можно получить только в случае, если оба партнера обладают точной информацией о часах своего рождения и сам расчет производит астролог-профессионал вручную, а не упрощенный онлайн-скрипт на сайте.

наглядная схема и 2 правила

Какие знаки считаются совместимыми?

Во всех гороскопах обязательным пунктом идет описание совместимости знаков, но, к сожалению, большинство из них описывает только частные случаи
на примерах пар знаков, упуская из виду общие принципы для всех. Хотя эти принципы являются очень логичными и вместе с тем простыми. А их понимание
поможет вам один раз и навсегда разобраться, кто, с кем и, что немаловажно, как совместим.

Итак, согласно классической астрологии, чьими принципами руководствуется расчет совместимости In-contri в соответствующем разделе,
знаки Зодиака подходят друг другу в любви и семейных отношениях, если они не противоречат 2 главным правилам:

знаки принадлежат одной четности
знаки не одинаковы

Соответственно, из первого пункта следует, что знаки принадлежат одной стихии или разным, но дополняющим друг друга. Стихий, как известно,
всего 4 — это Огонь, Земля, Воздух и Вода. Т.о. внутри каждой стихии знаки совместимы между собой и совместимы пары, представляющие позитивное
сочетание стихий Огонь-Воздух и Земля-Вода. Как видите, все просто.

2 группы совместимых знаков

Возьмем знаки с их стихиями по порядку и рассмотрим наглядно:

Овен (Огонь)
Телец (Земля)
Близнецы (Воздух)
Рак (Вода)
Лев (Огонь)
Дева (Земля)
Весы (Воздух)
Скорпион (Вода)
Стрелец (Огонь)
Козерог (Земля)
Водолей (Воздух)
Рыбы (Вода)

Мы видим, что знаки стихий Огня и Воздуха — нечетные, а знаки Земли и Воды — четные. Следовательно, совместимость знаков каждой пары стихий как между собой так и внутри очень естественна:
Воздух помогает Огню разгораться сильнее, а Вода наполяет Землю, делая ее плодородной.

Совместимые знаки Огня и Воздуха:
Овен, Лев и Стрелец — Близнецы, Весы и Водолей

Совместимые знаки Земли и Воды:
Телец, Дева и Козерог — Рак, Скорпион и Рыбы

С другой стороны, в комбинациях знаков разной четности — это пары стихий Вода-Огонь, Вода-Воздух, Земля-Огонь,
Земля-Воздух — позитивного союза не наблюдается. Более того, даже из природы стихий понятно, что некоторые из таких пар являются противоборствующими. Поэтому их совместимость в любви и семье
считается негативной.

Так работает совместимость знаков Зодиака в общем виде на уровне совместимы/несовместимы. Но есть еще ряд характерных особенностей, зависящих от взаимного расположения пары знаков.

7 типов совместимости между знаками

Более детальное описание совместимости в паре можно узнать по расположению знаков относительно друг друга на зодиакальном круге. Причем, как по часовой стрелке, так и против.
Только в зависимости от направления счета роль вашего знака в паре будет меняться. Разберем, как это работает, на примере первого знака — Овна.

Расположение: +1 и -1 знак от вашего
Тип пары: «Лучший друг и лучший враг» — несовместимость
Примеры: Овен(1) — Телец(2), Овен(1) — Рыбы(12)
Описание: самая популярная пара знаков среди всех остальных.
Быстро заводят дружбу, но серьезным отношениям мешает конфликт
стихий. Частые проблемы: зависть, соперничество, разница интересов и целей в жизни.

Расположение: +2 и -2 знака от вашего
Тип пары: «Старший брат и младший брат» — совместимость
Примеры: Овен(1) — Близнецы(3), Овен(1) — Водолей(11)
Описание: пара знаков позитивно сочетающихся стихий. Здесь важно
понимание своих ролей каждым из партнеров. «Старший брат»
обычно превосходит «младшего» в возрасте, опыте или характере.

Расположение: +3 и -3 знака от вашего
Тип пары: «Покровитель и советник» — несовместимость
Примеры: Овен(1) — Рак(4), Овен(1) — Козерог(10)
Описание: пара знаков стихий, находящихся в конфликте, но умеющих
при желании находить точки соприкосновения. Увы, только
в деловой, но не в семейной сфере. Для них лучше выбрать общий бизнес, чем дом.

Расположение: +4 и -4 знака от вашего
Тип пары: «Ребенок и родитель | Ученик и учитель» — совместимость
Примеры: Овен(1) — Лев(5), Овен(1) — Стрелец(9)
Описание: прекрасная пара знаков одной стихии. «Родитель» должен проявить всю свою мудрость,
заботу и терпение — от него здесь зависит больше. «Ребенку» достаточно быть не слишком капризным и своенравным.

Расположение: +5 и -5 знаков от вашего
Тип пары: «Удав и кролик» — несовместимость
Примеры: Овен(1) — Дева(6), Овен(1) — Скорпион(8)
Описание: пара, о которой пишут любовные романы. Без хэппи-энда. Сначала буря чувств, и эмоций.
В конце — скука и усталость «удава», разбитое сердце «кролика». Советуем избегать, особенно, если «кролик» —
это ваш знак.

Расположение: +6 и -6 знаков от вашего
Тип пары: «Противоположности притягиваются» — совместимость
Примеры: Овен(1) — Весы(7)
Описание: как полюса магнита эти знаки такие разные, но и так же сильно их притяжение.
Данные отношения настоятельно рекомендуются только опытным и мудрым партнерам.
Молодежь делает много ошибок такой паре и редко в состоянии раскрыть весь ее потенциал.

Расположение: один и тот же знак
Тип пары: «Я и мое зеркало» — несовместимость
Примеры: Овен(1) — Овен(1)
Описание: часто встречающаяся пара у юных партнеров. Нет ничего проще,
чем завязать отношения, с таким же как ты. Но и нет впоследствии ничего
более унылого и раздражающего, чем видеть свои же недостатки рядом.

Теорема Пифагора Математическое видео для детей

ЧТО ТАКОЕ ТЕОРЕМА ПИФАГОРА?

Теорема Пифагора — это формула, связывающая длины катетов и длину гипотенузы в прямоугольном треугольнике. Формула: a ² +b ² =c ² . Вы можете использовать формулу, чтобы найти недостающую длину стороны. Вы также можете использовать формулу, чтобы увидеть, может ли заданный набор длин сторон образовать прямоугольный треугольник.

T чтобы лучше понять теорему Пифагора…

ЧТО ТАКОЕ ТЕОРЕМА ПИФАГОРА?.
Теорема Пифагора – это формула, связывающая длины катетов и длину гипотенузы в прямоугольном треугольнике. Формула: a2+b2=c2. Вы можете использовать формулу, чтобы найти недостающую длину стороны. Вы также можете использовать формулу, чтобы увидеть, может ли заданный набор длин сторон образовать прямоугольный треугольник.
Чтобы лучше понять теорему Пифагора…

ДАВАЙТЕ РАЗЪЯСНИМ!

Празднование дня рождения

Теорема Пифагора — это формула, которая показывает, как связаны длины сторон прямоугольного треугольника. Две более короткие стороны треугольника называются катетами. Одна нога имеет длину a, а другая длина b. Самая длинная сторона называется гипотенузой. Имеет длину c. Формула ² +b ² =c ² . Найдите длину c, если a = 3 и b = 4. 3 ² + 4 ² = 9 + 16 = 25. Итак, c ² = 25. Это означает, что c = 5. Попробуйте сами. : Для прямоугольного треугольника найдите длину гипотенузы, если a=5 и b=12.

Празднование дня рождения Теорема Пифагора — это формула, которая показывает, как связаны длины сторон прямоугольного треугольника. Две более короткие стороны треугольника называются катетами. Одна нога имеет длину a, а другая длина b. Самая длинная сторона называется гипотенузой. Имеет длину c. Формула: a2+b2=c2. Найдите длину c, если a = 3 и b = 4. 32 + 42 = 9+ 16 = 25. Итак, c2 = 25. Это означает, что c = 5. Попробуйте сами: для прямоугольного треугольника найдите длину гипотенузы, если a=5 и b=12.

Рампа для скейтборда

Нижняя часть рампы для скейтборда имеет длину 100 сантиметров. Высота пандуса 30 сантиметров. Какова длина рамповой части? Подставляем в формулу 30 и 100 и находим значение c. 30 ² + 100 ² = 900 + 10 000 = 10 900. Извлеките квадратный корень из 10 900, чтобы найти значение c. Результат иррационален, поэтому округлим, чтобы дать приблизительный ответ. с ≈ 104,4 сантиметра. Рампа рампы скейтборда имеет длину примерно 104,4 сантиметра. Попробуйте сами: Для прямоугольного треугольника найдите длину гипотенузы, если основание равно 6 м, а высота 7 м. Воспользуйтесь калькулятором и округлите ответ до десятых.

Рампа для скейтборда Нижняя часть рампы для скейтборда имеет длину 100 сантиметров. Высота пандуса 30 сантиметров. Какова длина рамповой части? Подставляем в формулу 30 и 100 и находим значение c. 302 + 1002 = 900 + 10 000 = 10 900. Извлеките квадратный корень из 10 900, чтобы найти значение c. Результат иррационален, поэтому округлим, чтобы дать приблизительный ответ. с ≈ 104,4 сантиметра. Рампа рампы скейтборда имеет длину примерно 104,4 сантиметра. Попробуйте сами: для прямоугольного треугольника найдите длину гипотенузы, если основание равно 6 м, а высота 7 м. Воспользуйтесь калькулятором и округлите ответ до десятых.

Пандус для собак

В конструкции пандуса для собак указано, что самая длинная сторона имеет длину 5 футов, а длина основания — 4 фута. Какая высота пандуса? Подставьте эти две длины в формулу. Вы можете заменить 4 на a или b. a ² +4 ² = 5 ² , поэтому a ² +16=25. Вычтите 16 с обеих сторон, чтобы изолировать a ² . а ² =9. Поскольку 3×3=9, а=3. Высота пандуса для собак составляет 3 фута. Попробуйте сами: Одна сторона прямоугольного треугольника имеет длину 6 футов. Гипотенуза имеет длину 10 футов. Какова длина другой стороны?

Пандус для собак В конструкции пандуса для собак указано, что самая длинная сторона имеет длину 5 футов, а длина основания — 4 фута. Какая высота пандуса? Подставьте эти две длины в формулу. Вы можете заменить 4 на a или b. a2+42=52, поэтому a2+16=25. Вычтите 16 с обеих сторон, чтобы изолировать a2. а2=9. Поскольку 3×3=9, а=3. Высота пандуса для собак составляет 3 фута. Попробуйте сами: одна сторона прямоугольного треугольника имеет длину 6 футов. Гипотенуза имеет длину 10 футов. Какова длина другой стороны?

Beehouse

Если у вас есть прямоугольный треугольник, то длины сторон делают это уравнение верным: a ² +b ² =c ² . Другой математический факт заключается в том, что если a ² +b ² =c ² , то треугольник прямоугольный. Например, три куска дерева разрезают на куски длиной 8 см, 15 см и 17 см. Могут ли эти три длины соединиться, чтобы получился пчелиный домик в форме прямоугольного треугольника? Самая длинная сторона равна 17, поэтому установите c=17. Установите a=8 и b=15 для ножек. Возводя эти числа в квадрат, мы получаем ² = 64, b ² = 225 и c ² = 289. Тогда сумма 64+225 равна 289. Поскольку a ² +b ² имеет то же значение, что и c ² , это означает, что три куска дерева могут образовать прямоугольный треугольник. Попробуйте сами: Могут ли длины 7 сантиметров, 24 сантиметра и 25 сантиметров составить прямоугольный треугольник?

Beehouse Если у вас есть прямоугольный треугольник, то длины сторон делают это уравнение верным: a2+b2=c2. Другой математический факт состоит в том, что если a2+b2=c2, то треугольник прямоугольный. Например, три куска дерева разрезают на куски длиной 8 см, 15 см и 17 см. Могут ли эти три длины соединиться, чтобы получился пчелиный домик в форме прямоугольного треугольника? Самая длинная сторона равна 17, поэтому установите c=17. Установите a=8 и b=15 для ножек. Возводя эти числа в квадрат, мы получаем a2=64, b2=225 и c2=289.. Тогда сумма 64+225 равна 289. Поскольку a2+b2 имеет то же значение, что и c2, это означает, что три куска дерева могут образовать прямоугольный треугольник. Попробуйте сами: могут ли длины 7 сантиметров, 24 сантиметра и 25 сантиметров составить прямоугольный треугольник?

СЛОВАРЬ ТЕОРЕМЫ ПИФАГОРА

Катеты

Две более короткие стороны прямоугольного треугольника, часто обозначаемые a и b.

Гипотенуза

Самая длинная сторона прямоугольного треугольника, часто обозначаемая c.

Теорема Пифагора

В прямоугольном треугольнике квадрат наибольшей стороны равен сумме квадратов двух меньших сторон. Это представлено формулой a ² + b ² = c ² .

Квадратный корень

Значение, которое при умножении само на себя дает число.

Иррациональное число

Число, в котором десятичные разряды идут бесконечно без какой-либо закономерности.

Обратная теорема Пифагора

Если три длины делают формулу ² + b ² = c ² верно, тогда три длины могут образовать прямоугольный треугольник.

ТЕОРЕМА ПИФАГОРА ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ

Когда можно использовать теорему Пифагора?

Когда мне известны длины двух сторон прямоугольного треугольника, и я хочу вычислить недостающую длину стороны.

Чем возведение в квадрат, как в

², отличается от удвоения, как в 2а?

а ² =а⋅а, тогда как 2а=а+а. Например, 3 ² =9 и 3×2=6.

Как бы вы нашли длину самой длинной стороны треугольника, если две более короткие стороны имеют размеры 6 единиц и 8 единиц?

Подставьте эти значения в теорему Пифагора, чтобы получить 6 ² +8 ² =c ² . Упростите до 100=c ² , а затем извлеките квадратный корень, чтобы получить 10 единиц.

Как изменились бы ваши расчеты, если бы один катет был равен 6 единицам, а гипотенуза — 8 единицам?

Я все еще могу заменить a на 6, но теперь я заменяю c вместо b на 8. Формула 6 ² +b ² =8 ² дает 36+b ² =64 или b ² =28. Точное значение представляет собой квадратный корень из 28, что составляет около 5,3 единиц, округленных до десятых.

Как теорема Пифагора может помочь вам найти расстояние на координатной плоскости?

Я рисую треугольник с гипотенузой вдоль диагонали, которую хочу измерить. Я считаю длины катетов и заменяю ими a и b в теореме Пифагора. Затем я могу решить для c, чтобы найти его длину.

Вернуться к уроку

геометрия — Теорема Пифагора касается расстояний или площадей?

Теорема Пифагора не утверждает, что для любого прямоугольного треугольника площадь квадрата, одна из сторон которого является гипотенузой, равна сумме квадратов длин катетов.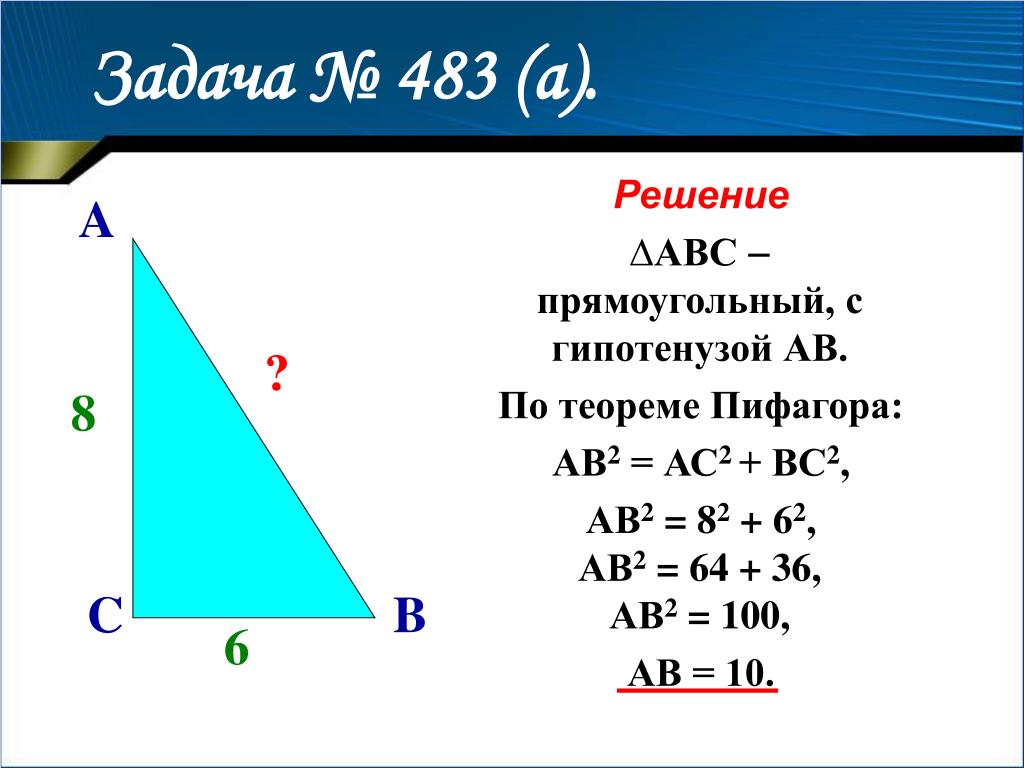 Теорема Пифагора утверждает, что для любого прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин катетов. Некоторые люди предполагают, что площадь любого квадрата равна квадрату длины его ребер, поэтому они принимают доказательство, подобное приведенному в этом ответе, как доказательство теоремы Пифагора. 92}$ из любой точки в любую другую точку, и поэтому теорема Пифагора верна для всех прямоугольных треугольников, оси которых параллельны осям. Это потому, что площадь можно определить с помощью исчисления. С дополнительным предположением вы можете показать, что теорема Пифагора верна для всех прямоугольных треугольников. Чтобы показать, что формула расстояния состоит в том, что даже при переходе от точки к самой себе, мы должны сделать дополнительное предположение, что расстояние от любой точки до самой себя равно 0,

92}$, вы действительно можете показать, что он удовлетворяет всем трем свойствам. Тривиально показать, что, используя это определение, расстояние от любой точки до самой себя равно 0. Это так называемое доказательство теоремы Пифагора показывает, что, используя это определение расстояния, площадь любого квадрата на самом деле равна квадрату длины его стороны. края. Также можно показать, что это определение удовлетворяет $\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R}\forall w \in \mathbb{R}d ((0, 0), (xz — yw, xw + yz)) = d((0, 0), (x, y))d((0, 0), (z, w))$ следующим образом. 92} = d((0, 0), (x, y))d((0, 0), (z, w))$

Вместо этого вы можете подумать, что нельзя допустить, что площадь любого квадрата равна квадрат длины его ребер и может только предположить, что формула расстояния удовлетворяет следующим свойствам:

$\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R}\forall w \in \mathbb{R}d((x, y), (x + z, y + w)) = d((0, 0), (z, w))$
$\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R}\forall w \in \mathbb{R}d((x, y), (z, w))$ неотрицательно
$\forall \text{ неотрицательное } x \in \mathbb{R}d((0, 0), (x, 0)) = x$
$\forall x \in \mathbb{R}\forall y \in \mathbb{R}d((0, 0), (x, -y)) = d((0, 0), (x, y ))$
$\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R}\forall w \in \mathbb{R}d((0, 0), (xz — yw, xw + yz)) = d((0, 0), (x, y))d((0, 0), (z, w))$

, но вы все еще видели доказательство теоремы Пифагора, подобное тому, что в этом ответе, и поэтому вы задались вопросом, была ли теорема Пифагора просто теоремой о площади, а не теоремой о расстоянии. На самом деле это теорема о расстоянии, и некоторые люди принимают это доказательство, потому что делают предположение, что площадь любого квадрата равна квадрату длины его сторон. 92}$ и, следовательно, площадь любого квадрата равна квадрату длины его ребер. Откуда мы знаем, что на самом деле существует способ определения расстояния, который удовлетворяет всем 5 этим свойствам? Поскольку показать, что функция, удовлетворяющая первым четырем свойствам, несложно, ранее было показано, что эта функция также удовлетворяет свойству 5. Теперь мы знаем, что, поскольку она удовлетворяет этим свойствам, она также удовлетворяет и тому свойству, что площадь любого квадрата равна площади любого квадрата. квадрат длины его ребер.

Есть еще одно свойство расстояния, которое некоторые люди находят настолько интуитивным, что я никогда не упоминал ранее. Это означает, что $\forall x \in \mathbb{R}d((0, 0), (\cos(x), \sin(x))) = 1$. Откуда мы знаем, что функция также удовлетворяет этому дополнительному свойству? Потому что это можно доказать следующим образом.